Натуральные числа: бесконечное множество возможностей
Узнай, почему натуральные числа никогда не заканчиваются! Бесконечное множество возможностей ждет тебя в мире математики. Открой для себя тайны натуральных чисел!
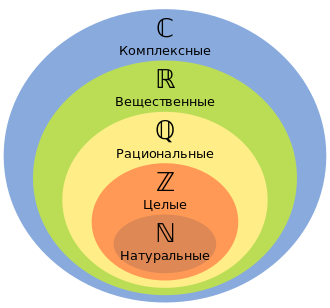
Натуральные числа – это основа математики‚ числа‚ которые мы используем для счета предметов. Они кажутся простыми и понятными‚ но скрывают в себе глубокие математические концепции. Вопрос о том‚ сколько существует натуральных чисел‚ является одним из фундаментальных в математике. Ответ на него‚ возможно‚ удивит тех‚ кто только начинает изучать эту науку‚ ведь множество натуральных чисел бесконечно. Это означает‚ что не существует самого большого натурального числа‚ и к любому числу можно прибавить единицу‚ получив следующее натуральное число.
Что такое натуральные числа?
Натуральные числа – это числа‚ используемые для счета. Традиционно к ним относят все целые положительные числа‚ начиная с единицы (1‚ 2‚ 3‚ …). Однако‚ существует дискуссия о включении нуля (0) в множество натуральных чисел. В некоторых областях математики‚ например‚ в теории чисел‚ ноль не считается натуральным числом‚ в то время как в других областях‚ таких как теория множеств‚ он может быть включен.
Основные свойства натуральных чисел
- Бесконечность: Множество натуральных чисел бесконечно.
- Упорядоченность: Натуральные числа можно упорядочить по возрастанию.
- Дискретность: Между двумя последовательными натуральными числами нет других натуральных чисел;
Сколько их существует?
Ответ на вопрос‚ вынесенный в заголовок‚ прост: бесконечно много. Математически это обозначается символом ∞ (бесконечность). Это означает‚ что мы никогда не сможем перечислить все натуральные числа‚ потому что всегда можно найти число больше‚ чем любое уже названное.
Применение натуральных чисел
Натуральные числа находят широкое применение в различных областях:
- Счет и измерение: Самое очевидное применение – счет предметов и измерение величин.
- Компьютерные науки: Используются для индексации массивов‚ адресации памяти и других задач.
- Криптография: Натуральные числа играют важную роль в алгоритмах шифрования.
- Теория чисел: Изучение свойств натуральных чисел является одной из центральных задач этой области математики.
Сравнение множеств натуральных и целых чисел
| Характеристика | Натуральные числа | Целые числа |
|---|---|---|
| Определение | Положительные целые числа (иногда с нулем) | Все целые числа (положительные‚ отрицательные и ноль) |
| Минимальное число | 1 (или 0‚ в зависимости от определения) | Не существует (отрицательная бесконечность) |
| Бесконечность | Да | Да |
| Примеры | 1‚ 2‚ 3‚ 4‚ 5… | …‚ -3‚ -2‚ -1‚ 0‚ 1‚ 2‚ 3… |
Таким образом‚ натуральные числа представляют собой фундаментальное понятие в математике‚ лежащее в основе многих других концепций. Их бесконечное количество делает их неисчерпаемым источником для исследований и открытий. Понимание свойств натуральных чисел необходимо для изучения более сложных разделов математики и их применения в различных областях науки и техники. Их простота и в то же время бесконечность делают их удивительным объектом изучения. Именно благодаря этим числам мы можем считать‚ измерять и описывать мир вокруг нас.